Waarom een konijn de perfecte gulden snede is

Professor Jean Paul Van Bendegem, filosoof en wiskundige (VUB), bijt de spits af met een wel heel humoristische kijk op het onderwerp. Philippe Van Cauteren, directeur van het SMAK, getuigt vervolgens over een zeer persoonlijke reiservaring. Hij heeft het over de altijd aanwezige schoonheid, zelfs te midden van de grootste ellende.

Wat is de gulden snede precies?

Wikipedia beschrijft de gulden snede als de verdeling van een lijnstuk in twee delen in een speciale verhouding. Die verhouding wordt het gulden getal genoemd en aangeduid met de Griekse letter φ (uitgesproken als phi). De wiskundige eigenschappen van de gulden snede werden al in de oudheid bestudeerd. De term zelf dateert uit de jaren 30 van de 19e eeuw. De gulden snede bezit een intrinsieke schoonheid en komt veel voor in de klassieke architectuur en schilderkunst. Ook het ideale menselijke lichaam zou volledig volgens de guldensnedeverhouding zijn opgebouwd. In de loop van de 20e eeuw verwierf de gulden snede een plaats in het kunstonderwijs en de fotografie. Kort samengevat? De gulden snede creëert een goed gebalanceerd beeld waarbij de kijker sneller tot de kern komt en een betere esthetische ervaring heeft.

Jean Paul van Bendegem legt de gulden snede uit

We gebruiken een aantal van zijn slides om zijn wiskundige redenering aan te tonen. Helaas kunnen we zijn humor niet zo visueel weergeven, maar dat er gelachen werd, is een feit. Dat Van Bendeghem, laten we hem Jean Paul noemen, de gulden snede wiskundig enorm boeiend en intrigerend vindt, werd al snel duidelijk.

Hij ging rustig van start met een vergelijking die een bepaalde verhouding én een bepaalde groei weergeeft. Na een uitleg over het meetkundig en rekenkundig gemiddelde – maar daarmee vervelen we je niet – bereikte hij de volgende conclusie: φ = 1 + √5 / 2.

Als iemand dus zegt dat hij een gulden snede ziet, dat moet je hem vragen: “Oh ja? Waar zit de vierkantswortel van 5 dan?” De √5 is trouwens gelijk aan 1,62…. (afgerond cijfer).

De rare eigenschappen van de gulden snede

Wat volgt is er alvast één van die rare eigenschappen. Let op de volgende logische cijferreeks.

• Phi tot de 3de macht = 2 x phi + 1
• Tot de 4de macht = 3 x phi + 2
• En tot de 5de = 5 x phi + 3

Verhouding is één ding, groei een ander. Bekijken we het hart van een zonnebloem dan zien we twee soorten spiralen: 21 met de klok mee, 34 tegen de klok in. Ook deze cijfers moeten we in het achterhoofd houden: 1 2 3 4.

Verder wijst Jean Paul ook op het bestaan van de gouden hoek met als waarde 136,508…° Dat cijfer komt overeen met de optimale stapeling van alle pitten in het hart van een zonnebloem en wijst op optimale groei en perfectie in de natuur. De meeste zonnebloemen zijn echter niet zo perfect als deze. De evolutie zorgt voor voldoende afwijkingen, ook bij de mens.

De overbekende schelp

De overbekende schelp is het gevolg van een wonderbaarlijke ontwikkeling in de loop der tijden, en tegelijk een perfecte verhouding van groei en schaal die wiskundig zeer diep gaat. De schelp toont als het ware een gulden rechthoek aan. Vanaf de middeleeuwen werd deze perfecte verhouding overal toegepast. Denk aan het Parthenon en de universele man van Leonardo. De Marquart Beauty analysis toont echter aan dat bepaalde theorieën heel vlug kunnen ontsporen. Op de Marquart-website kan je een masker downloaden dat volledig bestaat uit gulden snedes. Wie dit masker voor zijn gezicht plaatst, ziet meteen hoe ideaal en perfect zijn gezicht is. Even wat hilariteit tussendoor. Er bestaat zelfs een app die het omgekeerde doet en je foto aanpast aan het masker. De foto van Trump is daar een hilarisch voorbeeld van.

Terug naar het idee van de groei

Fibonacci heeft het in een van zijn geschriften over konijnen. In het begin van de 13de eeuw was wiskunde vooral meetkunde. Toen de algebra binnenkwam vanuit de Arabische wereld zag Fibonacci meteen in dat deze methode véél wiskundige problemen kon oplossen. Een ervan was het probleem van voortplanting van konijnen. Lees even mee.

• De eerste maand heb je één paar jonge konijnen.
• Een paar is volwassen vanaf de tweede maand.
• Een volwassen paar krijgt elke maand één paar nakomelingen.
• De konijnen sterven niet.

Vraag: hoeveel konijnen zijn er na n maanden? Jean-Paul heeft het over K1, K2, K3 (hilariteit) en komt uiteindelijk tot de volgende veralgemening: K(n) = K(n-1) + K(n-2)

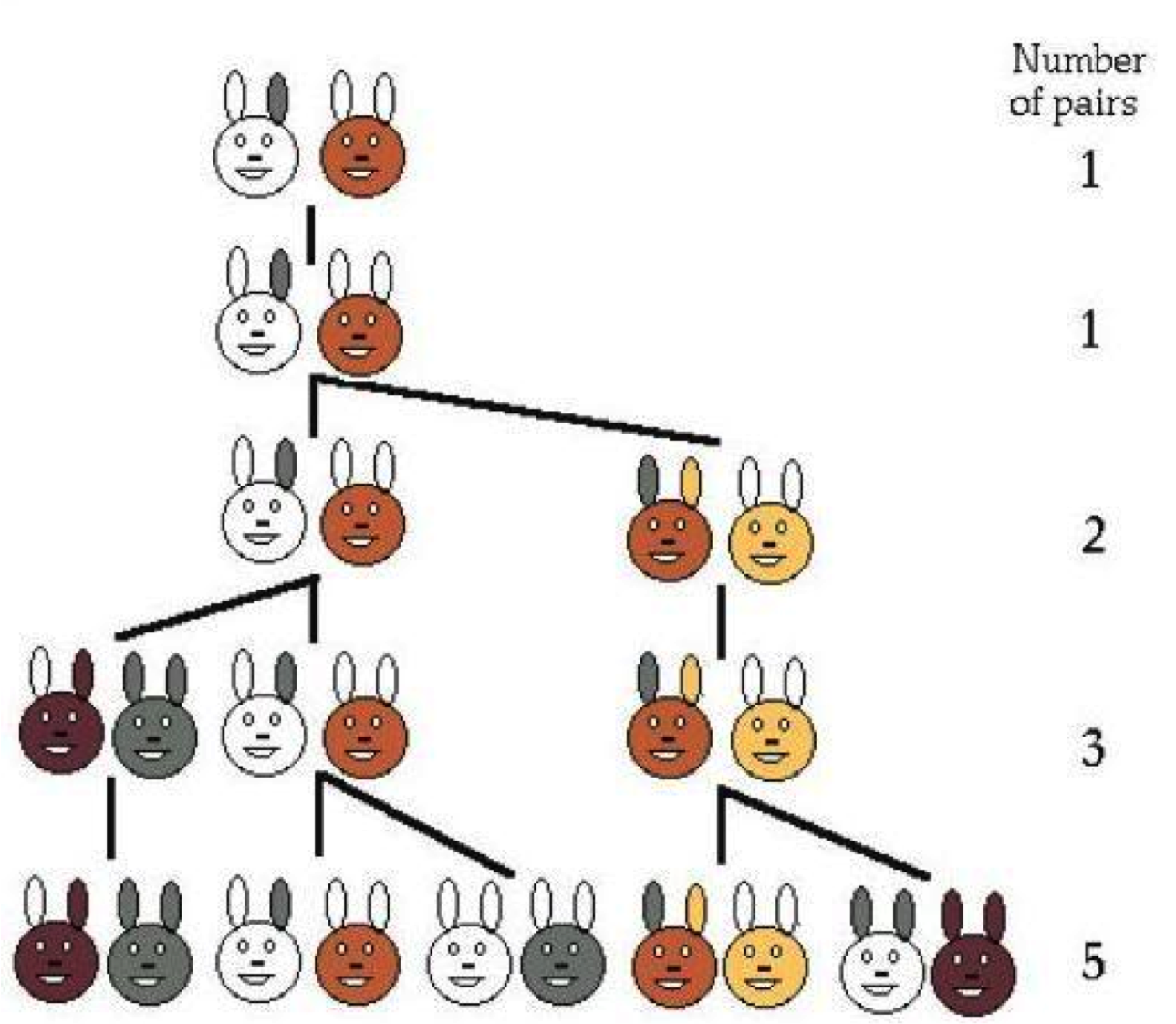
En zo komt Fibonacci tot zijn rij

Het aantal konijnenparen in een willekeurige maand is het aantal paren van de vorige maand plus het aantal vruchtbare paren in de maand ervoor. En zo verkrijg je een cijferreeks: de rij van Fibonnaci: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … Wie goed kijkt ziet hier dezelfde cijfers voorkomen als bij de gulden snede.

De verhouding van twee opeenvolgende konijnengeneraties duidt de groei aan: K(n) / K(n-1).
De verhouding van het aantal konijnenparen tegenover het aantal paren in de maand ervoor is dus de groeifactor.
Als uitkomst krijg je het volgende: 1; 2; 1,5; 1,66; 1,6; 1,625; 1,615; 1,619; 1,618; ….
Het getal wordt constant en zal dat min of meer blijven in de toekomst.

Waaraan is de G van groeifactor dan gelijk?

Na een ingewikkelde berekening komt Jean-Paul uit op: G =1 + √5 / 2. G is dus de gulden snede! Wat toont dit aan volgens Jean-Paul? We gebruiken zijn woorden: “Konijnen neuken zich naar de perfectie. Vergelijk dat met de mens! Dan besef je ten volle dat die geen toekomst heeft. Mijn tip? Zie je konijnen bezig? Zeg dan: Respect! Want jullie zijn een gulden snede aan het maken”.

Om af te sluiten verwijst Jean-Paul naar het boek van Darcy Thompson, ‘On Growth and form’. Daarin toont hij aan dat naast alle groeiprocessen waar de specifieke verhouding van de gulden snede een rol speelt, er nog veel andere groeiprocessen zijn waar andere verhoudingen een rol spelen. De gulden snede is dus belangrijk, maar niet zo belangrijk als men doorgaans denkt.

En toen was het de beurt aan Philippe Van Cauteren

Na de wiskundige reis van Jean Paul van Bendegem brengt Philippe Van Cauteren een persoonlijke reflectie over de gulden snede. Hij neemt ons mee op een heel andere reis. Die start met een tekening die een kind kan hebben gemaakt. Het lijkt Lovendegem wel, je ziet een huis, bloemen, een grasveld, de zon schijnt. De tekening is echter niet gemaakt door een kind, ook niet door een volwassene van hier, en het is ook Lovendegem niet. De tekening is gemaakt door een volwassen vluchteling in Afghanistan. Van Cauteren laat veel tekeningen zien, allemaal het resultaat van een ontmoeting in december 2014 met mensen die op de vlucht waren voor IS. Van Cauteren heeft hen gevraagd een tekening te maken. Hij is er immers van overtuigd dat mensen in nood toch aan de slag kunnen met een blad papier, potlood, penseel, stift, en daarmee een spoor van schoonheid kunnen achterlaten.

Curator Irak op Biënnale van Venetië

In 2014 werd Van Cauteren gevraagd om voor de Biënnale van Venetië het paviljoen van Irak samen te stellen. Een enorme uitdaging, niet het minst omdat Irak geen traditie heeft in Venetië. Van Cauteren organiseerde een reis naar Bagdad om daar kunstenaars op te zoeken, maar kon niet voorzien dat IS er in 2014 een kalifaat zou stichten. Hij kwam terecht in de ellende van drie vluchtelingenkampen en vroeg de vluchtelingen een tekening te maken als manier om te communiceren. “Iedereen denkt dat de noden in een vluchtelingenkamp uitsluitend gaan naar eten, dekens en kledij. Maar de behoefte van de mensen om zich uit te drukken blijft bestaan.” Van Cauteren verzamelde driehonderd tekeningen. Sommige ervan doen heel kinderlijk aan maar tonen vooral schoonheid, er is heel weinig verdriet en geweld te zien. Eén tekening toont een pen onder een Arabische tekst: “Mijn pen begon te huilen, voordat ik zelf in tranen uitbarstte.”

Mensen willen sporen nalaten

Ook vluchtelingen willen sporen nalaten, zelfs in de meest ellendige omstandigheden. Voor ons deden ze dat in de vorm van tekeningen. We wilden die tekeningen een stem en een gezicht geven en realiseerden samen met Ai Wei Wei het boek ‘Traces of Survival’, met een dubbel doel. We wilden de tekeningen bewaren als getuigenissen van een crisis, zonder artistieke ambities. Ten tweede wilden we de relatie bewaren die we toen in de drie kampen hebben opgebouwd. De opbrengst van de verkoop van het boek – 30.000 dollar – hebben we aan de drie kampen geschonken om projecten uit te werken met bewoners en residerende kunstenaars. “Tekeningen zijn een direct verband tussen ons denken en doen, deze menselijke uitingen benaderen het meest de schoonheid. Het is belangrijk om de schoonheid elders te zoeken dan waar we ze verwachten. In dit geval hebben we schoonheid gevonden in de heel eenvoudige en banale tekeningen van vluchtelingen. Is dit kunst? Neen, dit gaat voorbij de kunst”, aldus Van Cauteren.

Het vervolg? Van hier tot daar

De ervaringen in de kampen bleven maar in het hoofd van Van Cauteren rondspoken. In Gent ontstond het boek ‘Van hier tot daar’ op dezelfde spontane manier. Enkele medewerkers van het museum zijn volledig vrijwillig langsgegaan in het Maximiliaanpark en in Leopoldsburg. Daar hebben ze vluchtelingen bezocht en hen gevraagd tekeningen te maken. Die tekeningen fungeren als het ware als archiefstukken. Een tip van Van Cauteren: in het Amsab bevinden zich prachtige tekeningen van Spaanse vluchtelingen in Gent. Ook hier vind je de sporen van schoonheid. Kijken naar kunst doe je het best met de beide voeten op de aarde.